Separating metric perturbations in near-horizon extremal Kerr spacetimes

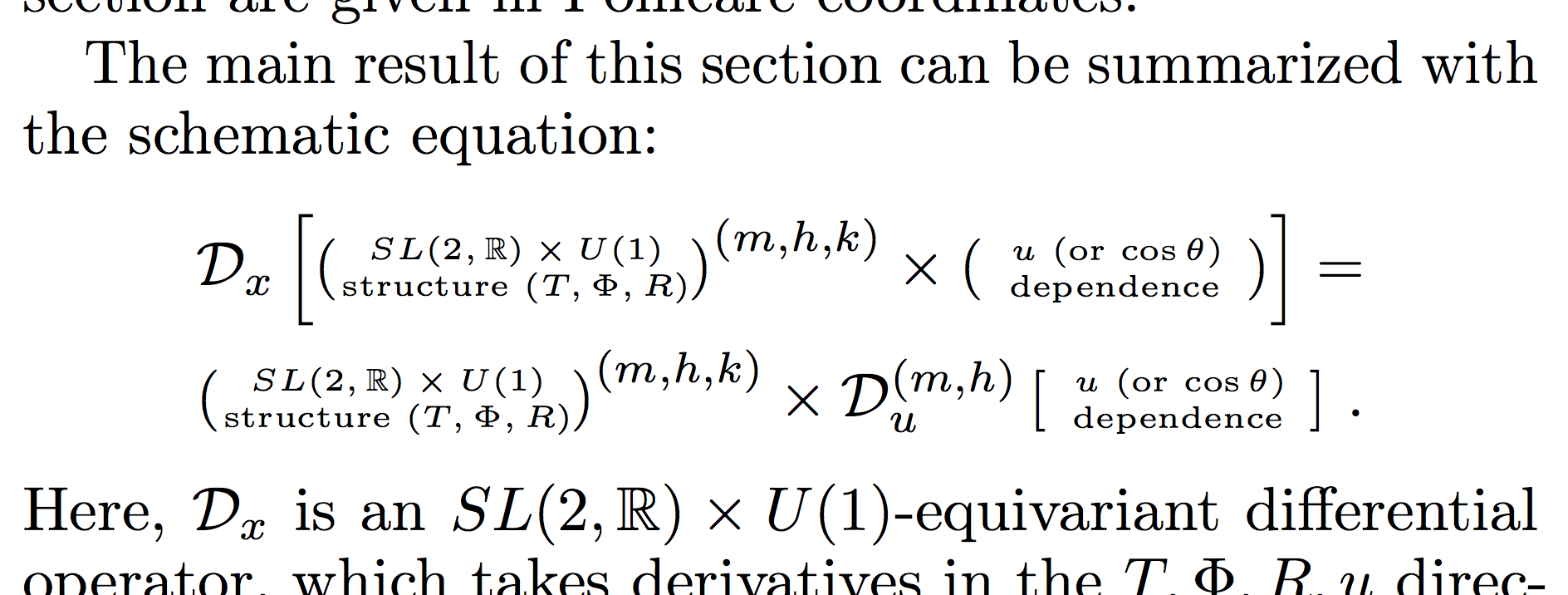
Linear perturbation theory is a powerful toolkit for studying black hole spacetimes. However, the perturbation equations are hard to solve unless we can use separation of variables. In the Kerr spacetime, metric perturbations do not separate, but curvature perturbations do. The cost of curvature perturbations is a very complicated metric-reconstruction procedure. This procedure can be avoided using a symmetry-adapted choice of basis functions in highly symmetric spacetimes, such as near-horizon extremal Kerr. In this paper, we focus on this spacetime, and (i) construct the symmetry-adapted basis functions; (ii) show their orthogonality; and (iii) show that they lead to separation of variables of the scalar, Maxwell, and metric perturbation equations. This separation turns the system of partial differential equations into one of ordinary differential equations over a compact domain, the polar angle.