The Principle of Stationary Nonconservative Action for Classical Mechanics and Field Theories

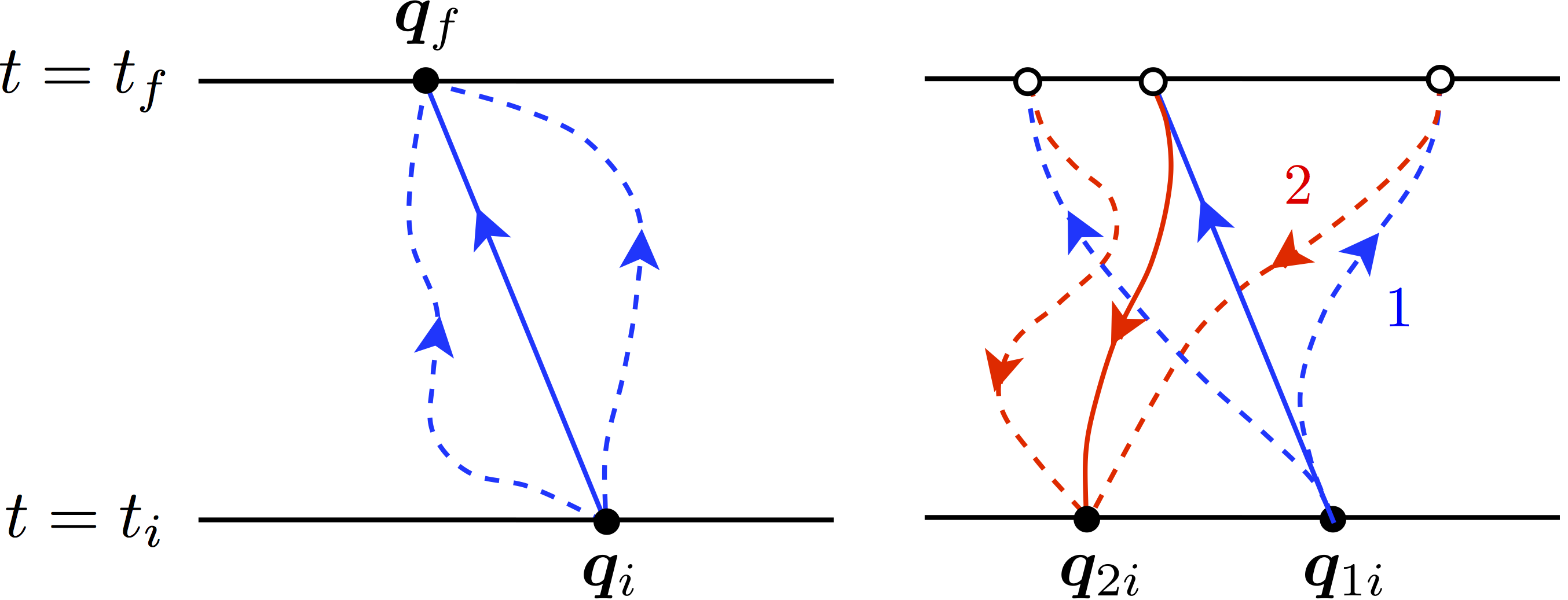
We further develop a recently introduced variational principle of stationary action for problems in nonconservative classical mechanics and extend it to classical field theories. The variational calculus used is consistent with an initial value formulation of physical problems and allows for time-irreversible processes, such as dissipation, to be included at the level of the action. In this formalism, the equations of motion are generated by extremizing a nonconservative action $\mathcal{S}$, which is a functional of a doubled set of degrees of freedom. The corresponding nonconservative Lagrangian contains a potential K which generates nonconservative forces and interactions. Such a nonconservative potential can arise in several ways, including from an open system interacting with inaccessible degrees of freedom or from integrating out or coarse-graining a subset of variables in closed systems. We generalize Noether’s theorem to show how Noether currents are modified and no longer conserved when K is non-vanishing. Consequently, the nonconservative aspects of a physical system are derived solely from K. We show how to use the formalism with examples of nonconservative actions for discrete systems including forced damped harmonic oscillators, radiation reaction on an accelerated charge, and RLC circuits. We present examples for nonconservative classical field theories. Our approach naturally allows for irreversible thermodynamic processes to be included in an unconstrained variational principle. We present the nonconservative action for a Navier-Stokes fluid including the effects of viscous dissipation and heat diffusion, as well as an action that generates the Maxwell model for viscoelastic materials, which can be easily generalized to more realistic rheological models. We show that the nonconservative action can be derived as the classical limit of a more complete quantum theory.