Parameter matching between horizon quasi-local and point-particle definitions at 1PN for quasi-circular and non spinning BBH systems in harmonic gauge

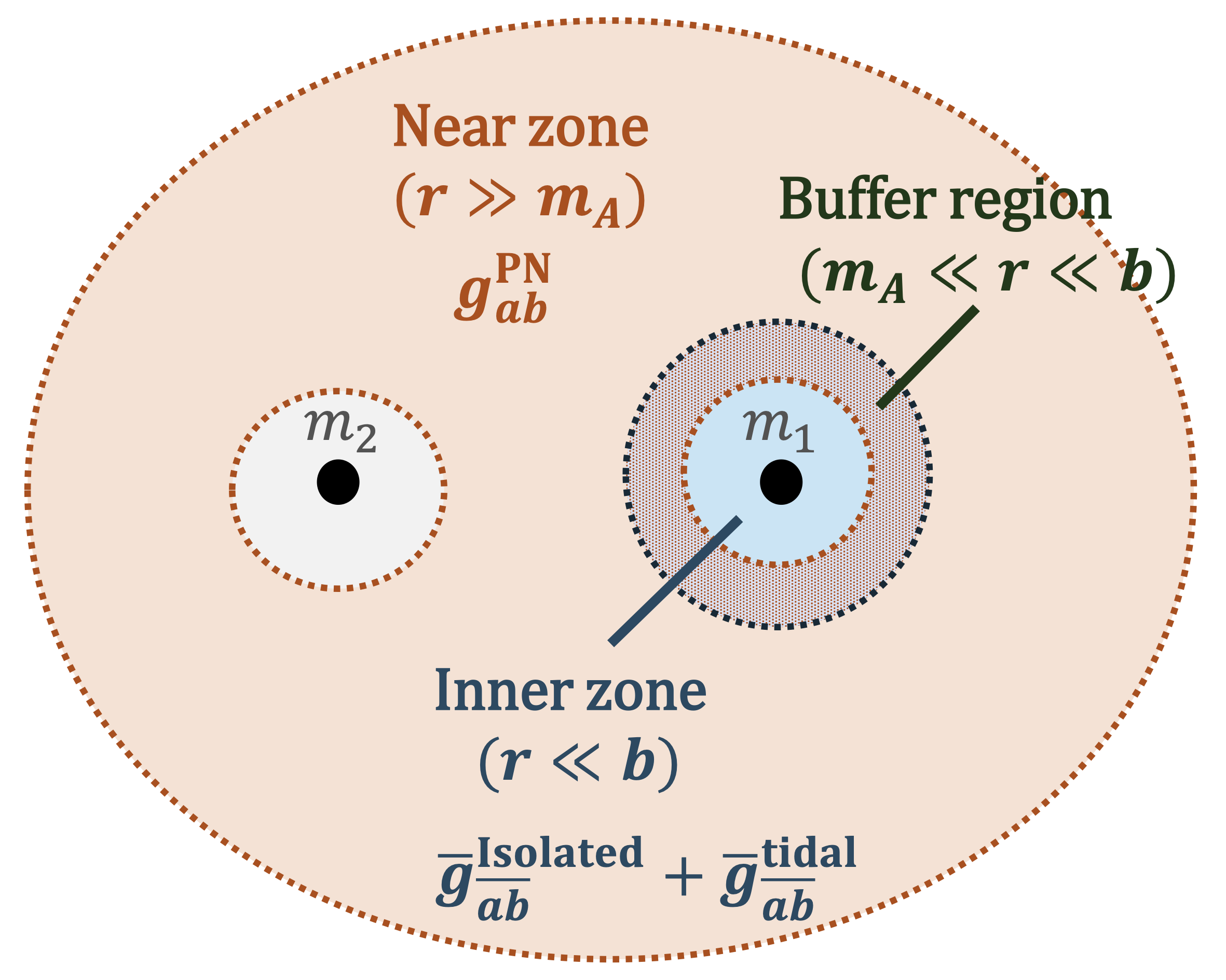
We investigate how commonly used parameter definitions in Post-Newtonian (PN) theory compare with those from Numerical Relativity (NR) for binary black hole (BBH) systems. In NR, masses and spins of each companion are measured quasi-locally from apparent horizon geometry, whereas in PN they are attributes of point particles defined via asymptotic matching in body zones. Although these definitions coincide in the infinite-separation limit, they could differ by finite-separation corrections that matter for precision modeling. Working entirely in harmonic gauge, we perform asymptotic matching between each companion’s inner zone metric – obtained from black hole perturbation theory – and the PN two-body metric, and construct the coordinate transformation that preserves the gauge in the strong field region. We solve perturbatively for the apparent horizon (AH) on a group of harmonic inertial time slice and compute its quasi-local areal mass from the horizon geometry. Then we establish the leading order matching between quasi-local (AH based) and PN (point-particle) parameter definitions in harmonic gauge. We find that on a horizon penetrating harmonic slicing, the AH quasi-local mass agrees with the PN point-particle mass at 1PN order. For generic harmonic slicings that deviate from the horizon penetrating condition by a 1PN order perturbation, the AH mass differs from the PN mass also by a 1PN correction. This parameter matching is crucial for hybridizing PN and NR waveforms and for providing better initial conditions in NR and Cauchy-Characteristic Evolution (CCE) simulations. The framework provides a bridge between different descriptions of BBH systems, and it can be extended to spinning and eccentric cases and more general NR gauges.