This question arose when I was discussing with Kaća Bradonjić, who has done work on gravity theories where conformal geometry plays a different role than in general relativity.

Just to be precise, here’s the question again. Let’s say we have an n-dimensional manifold M, and somebody hands you the metric $g_{ab}$. In all generality, the Riemann curvature of $\cd$ (the Levi-Civita connection of g) can have nonzero Ricci curvature and nonzero Weyl part (details below). Given this metric, can there exist a conformal factor $\Omega(x)>0$ such that the conformally transformed metric, $\tilde{g}_{ab} = \Omega^2 g_{ab}$, has zero Ricci curvature for its connection $\tilde{\cd}$?

First let’s recall the Ricci/Weyl decomposition of the Riemann tensor,

where the symbol $S_{r[abcd]}$ was one I used in this post to mean “project onto the algebraic symmetries of the Riemann tensor” by antisymmetrizing on ab, antisymmetrizing on cd, then symmetrizing on the two pairs. In Young tableau language, that means projecting with the Young symmetrizer that looks like

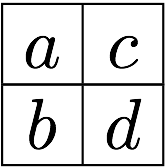
Next we have to crack open a textbook and look up how tensors that depend on $\tilde{g}_{ab}$ are determined by their counterparts from $g_{ab}$ and various derivatives of $\Omega$. You can find these in e.g. Appendix D of Wald.¹ The easy ones are

From Eq. \eqref{eq:confC} we immediately see that you can never get rid of Weyl curvature by conformal transformations (why the Weyl tensor is sometimes called the conformal tensor). Hence the most you can hope for is to be able to get rid of Ricci curvature through a conformal transformation.

The relationship between the Ricci tensors $\tilde{R}_{ab}$ and $R_{ab}$ is nastier. It’s slightly nicer to focus on a “trace-adjusted” version of Ricci called the Schouten tensor, which in components is

This happens to make the Ricci/Weyl decomposition \eqref{eq:R-decomp-proj} slightly simpler,

It also has a somewhat straightforward relationship under conformal transformations,

Notice that the trace of Schouten is determined by the trace of Ricci, $P = R/(2(n-1))$, so the vanishing of the Schouten tensor is equivalent to the vanishing of the Ricci tensor. Thus we can restate the original question to ask: when does there exist an $\Omega$ such that $\tilde{P}_{ab}=0$? And this immediately becomes a question of “integrability” of the system of equations

which are n(n+1)/2 partial differential equations for the single scalar field $\Omega$. For a gentle introduction to the theory of integrability from a geometric viewpoint, I recommend the sections on Frobenius’ theorem from Schutz’s little geometry book.²

To start with, we recast the second-order system \eqref{eq:integ0} in first order form by adjoining an auxiliary one-form

which must satisfy the integrability condition

by the commutativity of (torsion-free) covariant derivatives on a scalar field (i.e. the one-form $\omega$ is closed). In terms of this new one-form, Eq. \eqref{eq:integ0} becomes the first-order system of PDEs

If we can solve \eqref{eq:integomega1} for $\omega_a$ which satisfies \eqref{eq:integomega}, and there is no topological obstruction (i.e. $\omega$ is not just closed but exact; a question in de Rham cohomology), then it can immediately be integrated up into a solution for $\ln\Omega.$

Now to find the integrability of this first-order system, let’s take a further derivative $\cd_c$ of Eq. \eqref{eq:integomega1} and antisymmetrize over the [cb] index pair. On the left-hand side, this gives a commutator of covariant derivatives, which means we can convert it into a curvature tensor. The price is that on the right-hand side, we will be taking derivatives of the $\omega$’s. But if solutions exist, then we can just reuse \eqref{eq:integomega1} to replace $\cd\omega$ with P and products of $\omega$ without derivatives. I encourage you to do these manipulations with xAct/xTensor, of course.

The resulting integrability condition is the amazingly simple

As an easy consequence, when the Weyl tensor vanishes, $g_{ab}$ is conformal to Ricci-flat (and indeed conformal to flat) if and only if $\cd_{[a}P_{b]c} = 0$. This result was already known to Schouten back in 1920,³ but I’m interested in the more general case when the Weyl tensor is non-vanishing.

So, we have succeeded in turning integrability of \eqref{eq:integ0} into an algebraic test. In words, this condition is: Treat the Weyl tensor as a linear map from $T^*M$ to $T^*M^{\otimes 3}$; then a necessary (but not yet sufficient) condition for \eqref{eq:integ0} to be integrable is that $\cd_{[a}P_{b]c}$ must be in the image of this linear map.

At this point I would be remiss in my duties if I neglected to tell you that $\cd_{[a}P_{b]c}$ has a perhaps more familiar expression. Start from the Bianchi identity $\cd_{[a}R_{bc]de}=0$ and decompose Riemann into the Weyl and Schouten tensors. After performing a contraction, we find the identity

So we can see that $\cd_{[a}P_{b]c}$ lives in the representation labeled by the Young diagram In fact you could have seen this from the index symmetries without knowing identity \eqref{eq:divWeyl}.

Thus it is at least algebraically possible for $\cd_{[a}P_{b]c}$ to live in the image of $C: T^*M \to T^*M^{\otimes 3}$. If it actually does (which is the real question) then there is a space of potential solutions $\omega_d$ (unique up to elements of the kernel of Weyl). We then need there to be a solution in this space which satisfies the integrability condition $\cd_{[a}\omega_{b]}=0$. If all of these conditions are satisfied, then the closed one-form $\omega$ exists; and if there is no topological obstruction, $\omega$ is also exact, so $\ln\Omega$ may be integrated up, and finally $\tilde{g}_{ab}$ can be found, which will be Ricci-flat.

References